تاریخچه ی چرتکه

هزاران سال است که برای انجام محاسبات از چرتکه استفاده می­شود. محاسبه­ ی اعداد بزرگ­ همواره کاری دشوار تلقی می­شد به­ خصوص برای تاجرانی که از سطح سواد معمولی برخوردار بودند. این نیاز باعث شد تا ابزار چرتکه اختراع شود. ابزار چرتکه که مسائل ریاضی را با فرآیندی مکانیکی و سریع حل می­کند، با ماشین حساب­ های مدرن امروزی در رقابت است که چهار عملیات اصلی را انجام می­دهند. دانش­ آموزان پس از آشنایی با اصول اولیه ­ی محاسبات و حفظ کردن چند قانون ساده می­توانند برای حل مسائل مختلف از چرتکه استفاده کنند. امروزه، استفاده از چرتکه در کلاس­ های درس همچنان رواج دارد.

مقدمه

به خاطر سپردن اعداد کاری دشوار است. چگونه می توانید بدون قلم یا کاغذ اعداد را حفظ کنید؟ و یا اگر خواندن یا نوشتن ندانید، چگونه می توانید این کار را انجام دهید؟ چگونه می توانید بدون آگاهی از زبان نوشتاری، اعداد بزرگ را به درستی جمع، تفریق، ضرب یا تقسیم کنید؟ تمام این مسائل را می توان با استفاده از چرتکه حل کرد. چرتکه ابزاری محاسباتی است که برای جمع، تفریق، ضرب و تقسیم کاربرد دارد. تمام اعداد را می­توان بدون استفاده از قلم یا کاغذ با چرتکه محاسبه کرد. چرتکه به دو نوع اصلی تقسیم می­شود: نوع اول، لوحه­ هایی تخت و دارای سطحی مخصوص هستند که با سنگ یا لوبیا علامت­ گذاری می ­شوند . (شکل شماره­ ی 1). دومین نوع چرتکه با قاب و مهره درست می­ شود که مهره ­ها روی سیم یا میله قرار می­گیرند (شکل شماره ی 2). هردو چرتکه، کارکردی مشابه دارند.

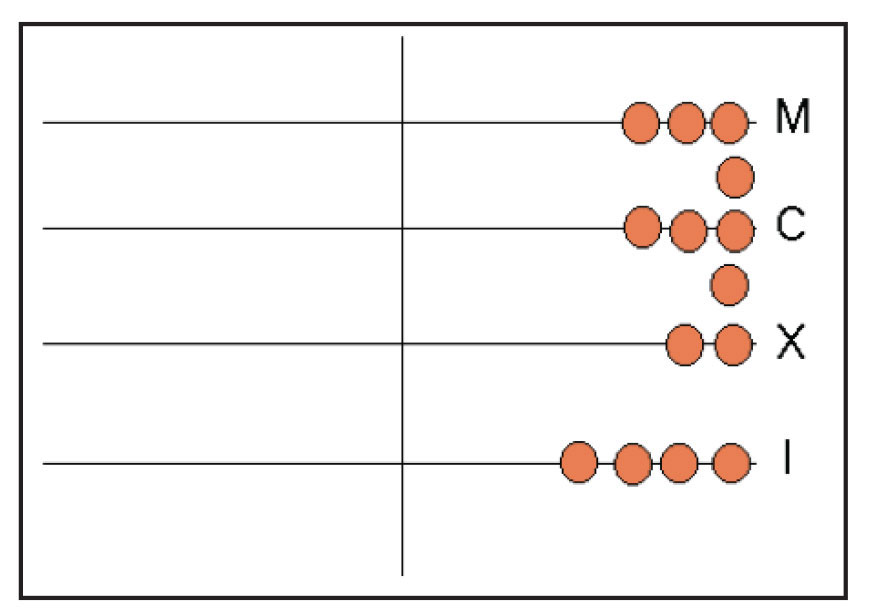
شکل شماره ­ی 1: جدول محاسباتی که عدد 3874 را نشان می­دهد.

استفاده از لوحه­ ها برای محاسبات به 2000 سال قبل یعنی دوران مصر و روم باستان برمی­گردد. اولین لوحه­ ها، تخته سنگ ­هایی ساده با خطوط موازی و افقی بودند که به عنوان شاخص­ های ارزش مکانی درنظر گرفته می­شدند. مصریان و رومیان باستان، محاسبات خود را با حرکت شمارشگرها روی تخته یا لوحی تخت انجام می­دادند که با خطوط یا نمادهایی علامت­گذاری می­شدند که “مکان” را نشان می­دادند (پولان، 1968، ص 18). تغییر حرکت خطوط افقی به خطوط عمودی ارزش مکانی، تنها تغییری بود که طی سال­ها در این تخته­ های محاسباتی اتفاق افتاد. منشا اختراع چرتکه ­های قاب­دار مشخص نیست. عده­ای بر این باورند که این چرتکه ­ها برای تاجرانی که دائم در سفر بودند، تولید شدند. برخی از مورخان، چینی­ ها را مخترعان این چرتکه ­های قاب­دار می­دانند و بعضی هم معتقدند که چینی ­ها پس از تجارت با رومیان با این چرتکه­ ها آشنا شدند (موون، 1971). کشورهای روسیه و ژاپن نیز چرتکه ­های منسوب به خود را از این طریق تولید کردند. امروزه، چرتکه در مناطق روستایی آسیا و آفریقا همچنان بدون محدودیت استفاده می­شود. کارکرد این ابزار به گونه ­ای است که تمام افراد می­توانند بدون استفاده از دستگاه ­های الکتریکی، اعداد بزرگ را محاسبه کنند. همان­طور که در بخش بعد عنوان خواهد شد، آسان بودن محاسبه با چرتکه موجب شده است تا افراد در هر سن و سالی بتوانند محاسبات خود را با این ابزار انجام دهند.

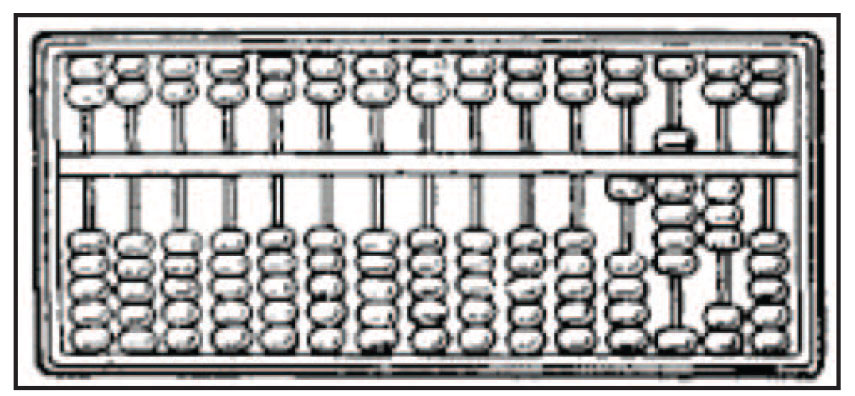
شکل شماره­ ی 2: چرتکه­ ی قاب­دار و مهره دار

تاریخچه­ ی چرتکه در جوامع باستان

بدیهی است که در تمدن­های باستان، محاسبات با ابزارهای مکانیکی انجام می­شدند. در دوران ماقبل تاریخ، بازرگانان از جداول محاسباتی خام استفاده می­کردند. از زمانی که فنیقی­ها، مصریان و یونانی­ ها تجارت را از طریق دریای مدیترانه آغاز کردند، چرتکه به ابزاری جهانی برای انجام محاسبات تبدیل شد (موون، 1971).

از آنجائی­که تاریخچه ­ی چرتکه مشخص نیست، منشا ابداع این ابزار را تنها می­توان حدس زد. تخته­ های محاسباتی قبل از چرتکه­ ها­ی مهره ­دار به کار گرفته می­شدند. این تخته­ ها به احتمال زیاد از میزهای چوبی ساخته می­شدند (پولان، 1968). هم­اکنون، برای آگاهی از تاریخچه­ ی چرتکه به بررسی نقاشی­ و ادبیات کلاسیک می­پردازیم؛ اما در این آثار تاریخی، تصویری از تاجران و بازرگانان طبقه ­ی پایین جامعه دیده نمی­ شود که اغلب از تخته­ های محاسباتی استفاده می­کردند. “به طور مثال، شاید باور این مسئله سخت باشد که افلاطون، مطالب خود را روی ابزاری می ­نوشت و این­کار را به بردگان یا خرده­ فروشان واگذار می­کرد” (موون، 1971، 21). به همین دلیل، در تاریخچه ­ی مصرو و روم، سخنی از چرتکه به میان نمی­ آید.

تخته­ محاسباتی  سالامیس

قدیمی ­ترین تخته­ ی محاسباتی حدود یک قرن پیش در جزیره­ ی سالامیس کشف شد (شکل شماره ­ی 3). برطبق بررسی­ های صورت گرفته، تاریخچه ­ی تخته­ ی محاسباتی به قرن چهارم پیش از میلاد مسیح بازمی­گردد (پولان، 1968). این تخته از سنگ مرمر سفید ساخته شده و ابعاد آن 4.5 × 75 × 149 بود. در قسمت بالای این تخته، هفت خط افقی قرار داشت که اعداد رومی کنار آن نوشته شده بودند. شمارشگرهای فلزی بین خطوط قرار داشتند و تعداد این شمارشگرها در هر خط، مقادیر مختلف را نشان می­داد. فضاهای عمودی برای نمایش واحدهای اصلی، دهگان، صدگان و غیره استفاده می­شدند و فضاهای میانی امکان علامت ­گذاری مقادیر بزرگ­تری مانند اعداد 50، 500 و غیره را برای کاربر فراهم می­کردند. این توضیحات در شکل شماره ­ی 3، مشاهده می شوند. با استفاده از این جداول مسائل جمع و تفریق به راحتی حل می­شدند. باگذشت زمان و مبادلات میان فرهنگی، چرتکه به صورت ابزاری سفارشی تکامل یافت که تمام نیازهای کاربر را برآورده می­ کرد.

شکل شماره ­ی 3: تخته­ ی محاسباتی سالامیس

 

تخته ­های محاسباتی قرون وسطی

در قرون وسطی تخته­ های محاسباتی تا قرن 16 در قاره­ ی اروپا کاربرد داشتند و از آن پس محاسبه با مداد و کاغذ جایگزین این تخته­ ها شد. پس از پیدایش روش­ های پیشرفته ­تر چاپ و نشر، کتاب­های ریاضی که تصاویری از تخته ­های محاسباتی در آن­ها مشاهده می­ شد، به اولین مستندات تبدیل شدند (موون، 1971). در تصاویر این کتاب­ ها اغلب دو ریاضیدان دیده می­ شد که یکی از آن­ها با استفاده از تخته ­ی محاسباتی و دیگری با مداد و کاغذ به حل معادلات مشغول بودند (تصویر شماره ­ی 4).

تخته ­های محاسباتی قرون وسطی به صورت عمودی قرار داشتند و هنگامی­ که کاربر اعداد را به سمت بالا حرکت می­داد، مقدار آن­ها افزایش می­ یافت. شمارش­گرها روی خطوط یا شیارهایی قرار داشتند که ارزش مکانی خاصی را نشان می­ دادند و مقادیر بزرگ­تر بین خطوط علامت­گذاری می­ شدند.

شکل شماره­ ی 4: ریاضیدانان با تخته ­ی محاسباتی و مداد و کاغذ درحال حل معادلات ریاضی هستند.

سایر انواع چرتکه ها

چرتکه­ ی دارای قاب و مهره و تخته­ ی محاسباتی از خصوصیات مشترک بسیاری برخوردار هستند اما ویژگی­ های خاص آن­ها بسته به فرهنگی که از آن استفاده می­شود، متفاوت است. تخته ­های محاسباتی نسبت به چرتکه­ های دارای قاب و مهره، انعطاف­ پذیری بیشتری دارند چراکه تعداد علائم این تخته­ نامحدود است، اما چرتکه ­ی دارای قاب و مهره، متراکم­تر، قابل حمل و با سرعت محاسباتی بیشتر است. در بخش ­های پیش­رو، به دلیل کاربرد گسترده ­ی چرتکه­ های مهره ­دار و خصوصیات منحصربه فرد انواع مختلف این چرتکه­ ها عنوان می­ شوند.

چرتکه ­ی رومی

چرتکه­ ی رومی از شمارشگرهای متحرک برخوردار است که به صورت موقت به دستگاه متصل شده­ اند. این چرتکه از صفحه­ ای فلزی با شمارشگرهای ثابت تشکیل شده است که روی میله ­ها حرکت می­کنند. هریک از میله های پایینی، چهار علامت­ دارد، اما میله ­ی سمت راست از پنج علامت­ برخوردار است. میله های بالایی نیز تنها یک علامت­ دارند. ارزش مهره­ ها در میله­ های بالایی پنج برابر مهره­ های پایینی است.

چرتکه­ ی چینی (سوآن پان)

“برخی بر این باورند که چرتکه­ ی رومی در اوایل دوران مسیحیت توسط بازرگانان به کشور چین وارد شد” (موون، 1971، ص 30). تا قرن دوازدهم، هیچ اسمی از چرتکه در مقالات چینی دیده نمیشد. سوآن پان به طور گسترده در کشور چین و سایر بخش­ های آسیا رواج داشته است. همان­طور که در شکل شماره ­ی 5 مشاهده می­شود، این چرتکه از پنج مهره در میله ­ی پایینی و دو “مهره­­ ی پنج­ تایی” در میله ­ی بالایی تشکیل شده است.

 

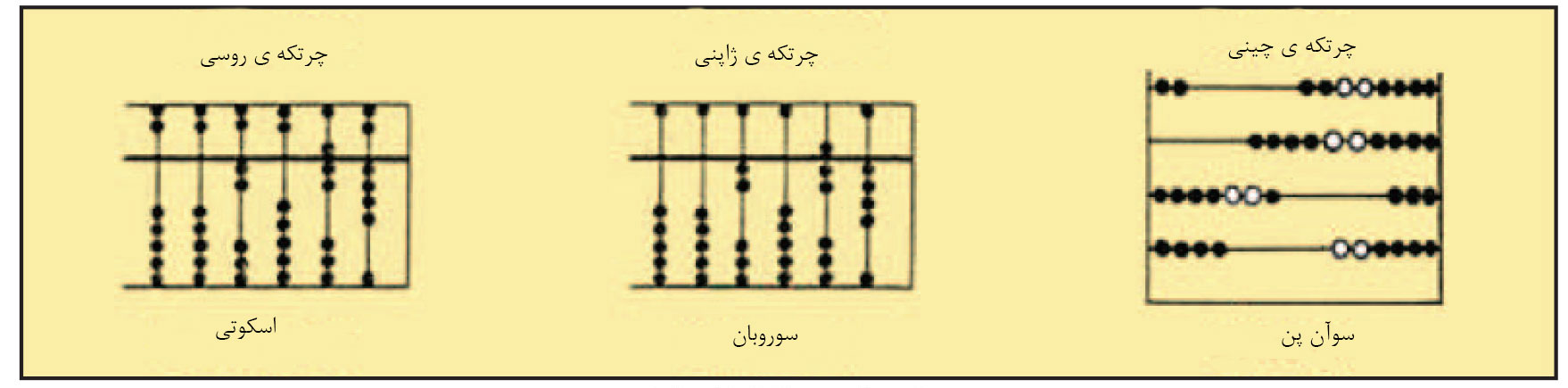
شکل شماره ­ی 5: انواع چرتکه­ ها

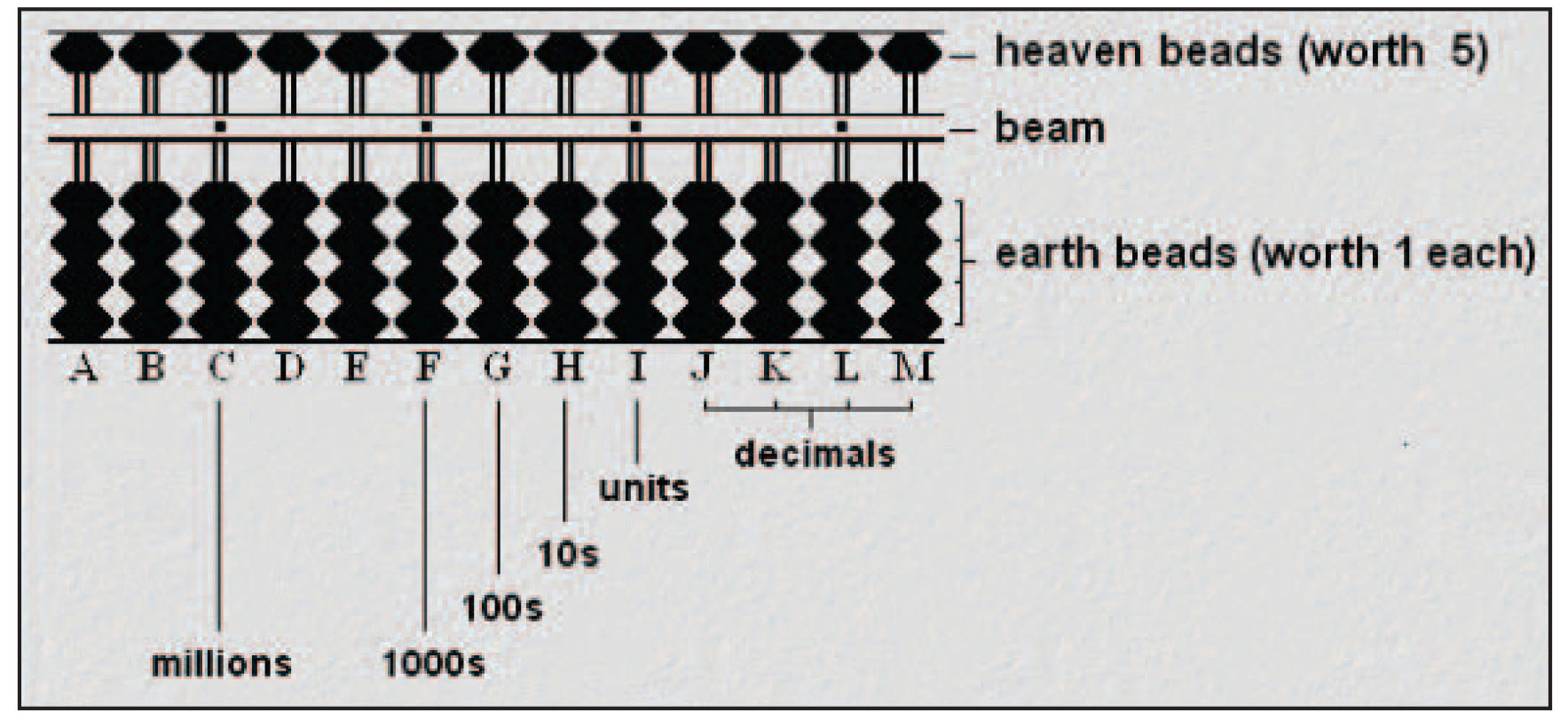
شکل شماره­ ی 6: چرتکه­ ی سوروبان

سوروبان

چرتکه ­ی پیشرفته­ ی ژاپنی که “سوروبان” نام دارد، به تقلید از چرتکه­ ی چینی (سوآن پان) ساخته شده است. در این چرتکه، چهار مهره در میله­ ی پایینی و یک مهره ­ی “پنج­ تایی” در میله­ های بالایی وجود دارد (شکل شماره­ ی 6). لبه­ ی مهره ­ها در چرتکه ­ی سوروبان تیز هستند که به راحتی در دست جای می­گیرند و فاصله ­ا­ی که برای حرکت آن­ها درنظر گرفته شده، تاحدی کم است که این مزیت باعث افزایش سرعت عملیات می­شود.

اسکوتی

در هر میله از اسکوتی که نوعی چرتکه­ ی روسی است، 10 مهره تعبیه شده و هیچ محور جداکننده ­ای در آن وجود ندارد (شکل شماره 5). این مسئله موجب می­شود تا تعداد زیادی مهره در فاصله ­ای نسبتا زیاد قرار داشته باشند. اما اعتقاد بر این است که یادگیری محاسبات با این نوع چرتکه آسان­تر از چرتکه­ های دارای مهره­ های با مضراب 5 است. باوجود آنکه تمام چرتکه ­هایی که پیش از این بررسی شدند، به صورت افقی عمل می­کنند، از چرتکه ­ی روسی می­توان به صورت عمودی نیز استفاده کرد (پولان، 1968).

کارکرد چرتکه

به طور کلی، کارکرد تمام چرتکه ­ها مشابه است. در این بخش، کارکرد چرتکه­ ی رایج سوروبان بررسی خواهد شد. چرتکه­ ی سوروبان برای سیستم شمارش ده تایی مناسب است که هر میله به عنوان نگهدارنده عمل می­کند و می­تواند مقادیر 0 تا 9 را نشان دهد. در هر میله از این چرتکه، یک مهره­ در بالا و چهار مهره در پایین قرار دارد (کوجیما، 1954). همان­طور که در شکل شماره ی 6 دیده می­شود، هریک از مهره ­های بالایی مضرابی از 5 و مهره­ های پایینی مضرابی از 1 هستند. شمارش مهره ­ها با بالا و پایین کردن آن­ها انجام می­شود.

پس از یادگیری نحوه­ ی شمارش با چرتکه، هر عدد صحیح را می­توان به آسانی روی آن نشان داد. قانون کلی این است که مقدار مشخص هر مهره­، 10 برابر مهره­ ی سمت راست یا یک نهم مهره­ ی سمت چپ آن است (کوجیما، 1954). اعداد اعشاری در سمت راست میله­ ی یکان قرار دارند (شکل شماره 6). در چرتکه­ ی سوروبان، برای انجام سریع و آسان محاسبات جمع و تفریق از دو قانون کلی استفاده می­شود. نخست، کاربر باید همیشه محاسبات را از چپ به راست انجام دهد (کوجیما، 1954). این کار ممکن است در ابتدا گیج­ کننده باشد، اما به تدریج سرعت عملیات بیشتر می­شود و با کمی تمرین می­توان محاسبه را به فرآیندی فنی و آسان تبدیل کرد. دوم اینکه، کاربر باید نحوه ­ی پیدا کردن اعداد متمم، به­ خصوص اعداد متمم 10 را فرا گیرد (کوجی ما، 1954). یک عدد متمم از طریق حل یک معادله­ ی ساده جمع به دست می­ آید. مقداری که به عدد اصلی اضافه می­شود تا عدد 10 به دست آید، عدد متمم نام دارد. برای نمونه، متمم عدد 7 نسبت به 10، 3 بوده و متمم عدد 6 نسبت به 10، 4 است.

عملیات جمع

برای انجام محاسبات جمع با چرتکه­ ی سوروبان هنگامی­که عدد موردنظر با مقداری بیش از 9 جمع می­ شود، باید از عملیات تفریق استفاده کرد. در این حالت، عدد متمم کم می­ شود و مهره­ ی 1 به بالاترین ارزش مکانی میله­ ی بعدی افزوده می­شود (هفلفینگر و فلوم، 2011). به عنوان نمونه، فرض کنید که قصد داریم تا عدد 8 را با 4 جمع کنیم. همان­طور که در تصویر شماره­ ی 7 مشاهده می ­شود، این فرآیند با نمایش عدد 4 روی میله­ ی یکان H آغاز می شود.

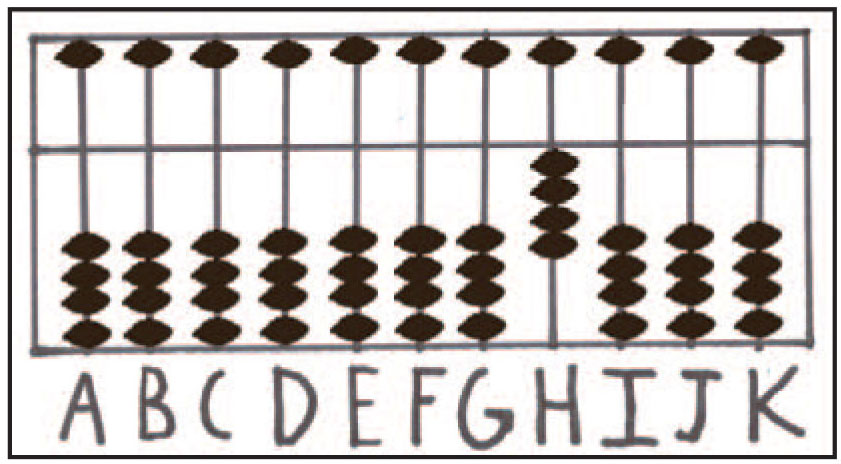شکل شماره ی 7: نمایش عدد 4 روی میله ی H

از آنجائی­که حاصل جمع این دو عدد (8+4) بیشتر از 9 است، پس باید از عملیات تفریق استفاده کرد. باید عدد متمم 8، یعنی عدد 2 از عدد 4 روی میله ­ی H کم شود و مهره ­ی 1 به میله­ ی دهگان G اضافه شود. این عملیات در شکل شماره­ ی 8 نشان داده شده است.

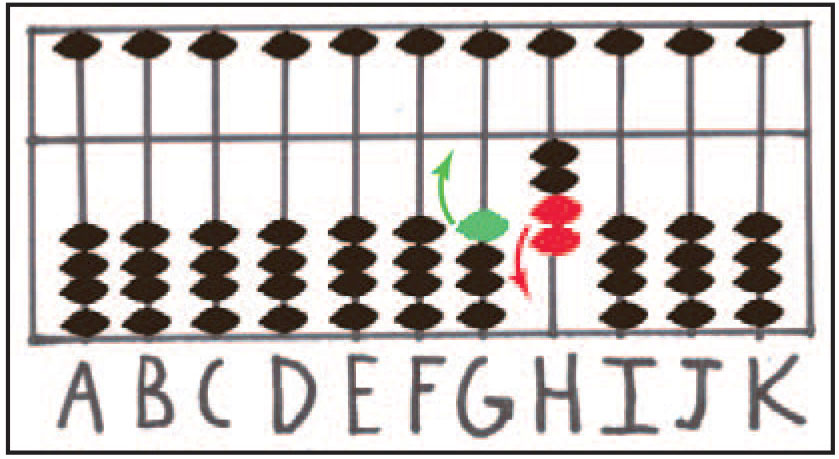شکل شماره ی 8: کم کردن عدد 2 و اضافه کردن 10

در این حالت، همان­طور که در شکل شماره­ ی 9 مشاهده می شود، یک مهره­ ی ده تایی روی میله G (میله ­ی دهگان) و دو مهره ­ی یکان روی میله ­ی H (میله­ ی یکان) باقی می­مانند. نتیجه نشان می ­دهد که حاصل جمع 4+8  برابر با 12 است.

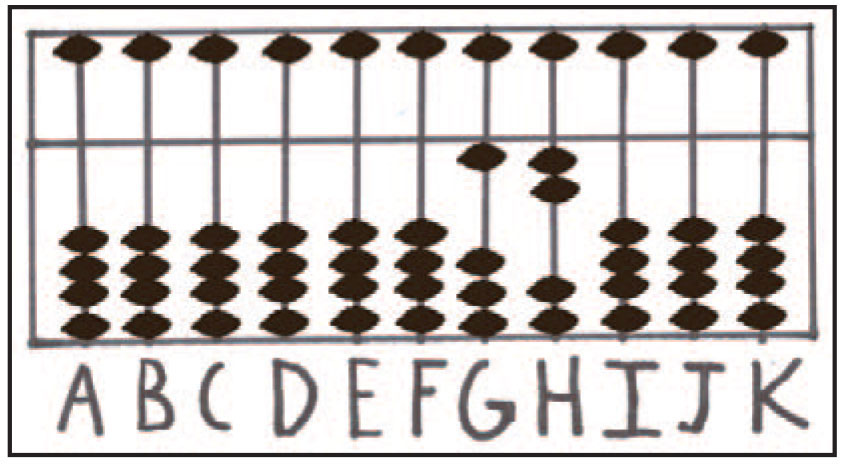شکل شماره ی 9: نتیجه ی نهایی عملیات 12=8+4

این قانون برای تمام اعداد صدق می­کند. به عنوان نمونه، مسئله ­ی 472+356 را در نظر بگیرید. نخست، عدد 356 را روی میله ­های F, G, H نشان دهید که باتوجه به شکل شماره ­ی 10، H میله­ ی یکان است.

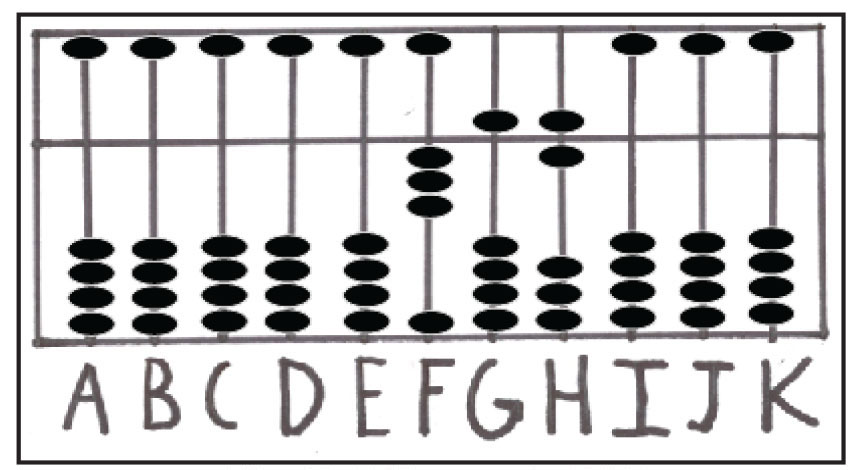شکل شماره ی 10: نمایش عدد 356 روی میله های F G H

به خاطر داشته باشید که عملیات از سمت چپ به راست انجام می­ شود. سپس، عدد 400 را به میله ی F اضافه کنید (عدد 5 را اضافه کرده و عدد 1 را کم کنید). حالا عدد 756 مانند شکل شماره ­ی 11 روی چرتکه نمایان است.

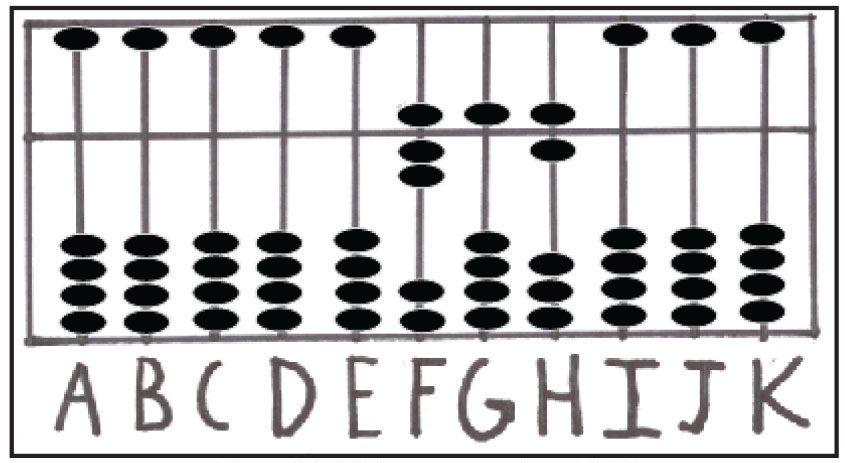شکل شماره ی 11: عدد 756 روی میله های FGH

حالا عدد 7 را روی میله­ ی دهگان G اضافه کنید. از آنجائی­که 9 < 7+5 است، پس متمم 7، یعنی عدد 3، از میله­ ی G کم شده و یک مهره­ به میله ­ی F اضافه خواهد شد. عدد نهایی یعنی 826 در شکل شماره­ ی 12 دیده می­ شود.

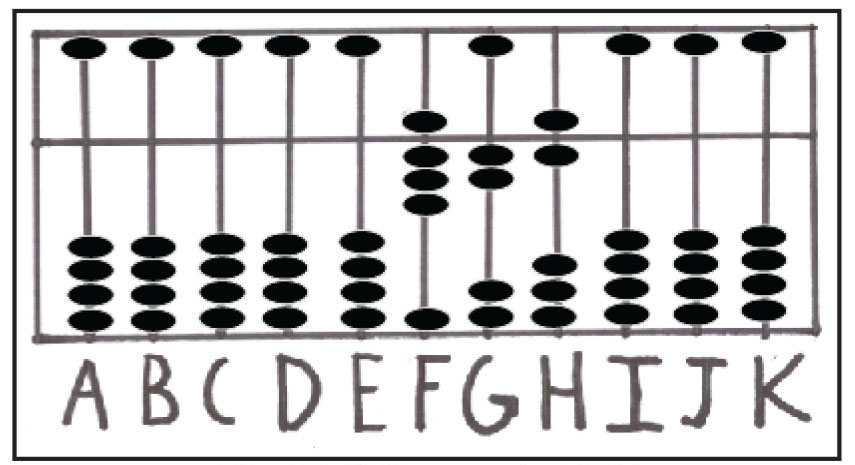شکل شماره ی 12: نمایش عدد 826 روی میله ای FGH

در مرحله­ ی آخر، عدد 2 به میله­ ی یکان H افزوده می­ شود. درنهایت، عدد 828 به دست می­ آید که در شکل شماره ­ی 13 نمایان است.

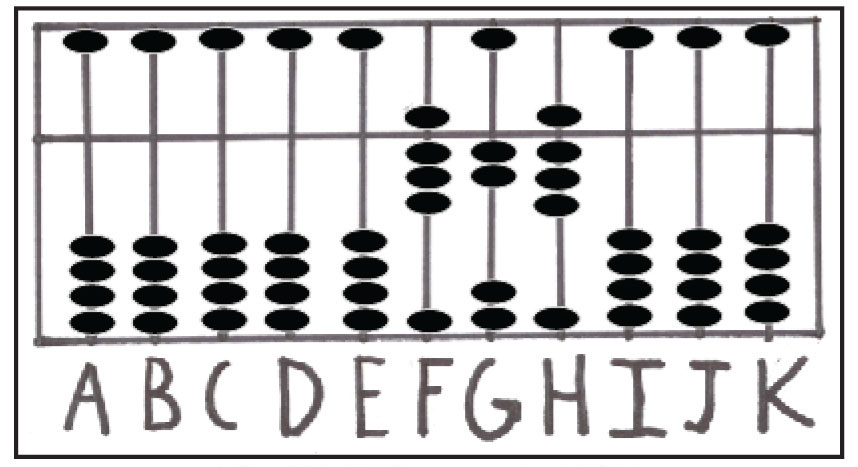شکل شماره ی 13: نمایش عدد 828 روی میله های FGH

عملیات تفریق

همان­طور که می­دانید، عملیات تفریق برعکس جمع است. از این­ رو، برای انجام عملیات تفریق با چرتکه ­ی سوروبان، عدد متمم را اضافه کرده و 1 مهره از میله­ ی بعدی کم می­ کنیم. به عنوان نمونه، برای کم­ کردن عدد 8 از 12 باید در ابتدا عدد 1 را روی میله­ ی دهگان G و عدد 2 را روی میله­ ی یکان H اضافه کنیم. از میله­ ی دهگان هیچ عددی کم نمی­ شود، بنابراین عدد 7 را از میله­ ی H کم می ­کنیم. از آنجائی­که 0 > 8-2 است، پس متمم 8 یعنی 2 به میله­ ی یکان H اضافه شده و یک مهره از میله­ ی دهگان G کم خواهد شد. این فرآیند در شکل شماره ­ی 14 نشان داده شده است. به این ترتیب، پاسخ این مسئله 4 خواهد بود.

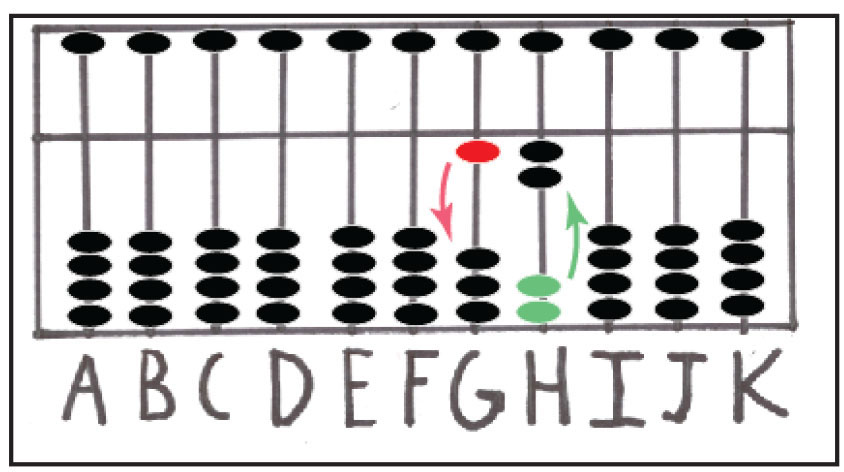شکل شماره ی 14: افزودن عدد 2 و کم کردن عدد 10

در مرحله ­ی بعدی، مسئله ­ا­ی پیچیده ­تر مانند 5361-6432  بررسی خواهد شد. نخست، عدد 6432 را روی میله­ های E, F, G, H نشان دهید که میله­ ی H یکان است (شکل شماره­ ی 15). سپس، عدد 5000 را از میله ­ی E کم کنید که در این صورت، عدد 1432 باقی می­ماند (شکل شماره 16). در این مرحله، عدد 30 را از میله­ ی F کم کنید. همان­طور که در شکل شماره 17 نشان داده شده است، حالا عدد 1132 روی چرتکه مشاهده می­ شود.

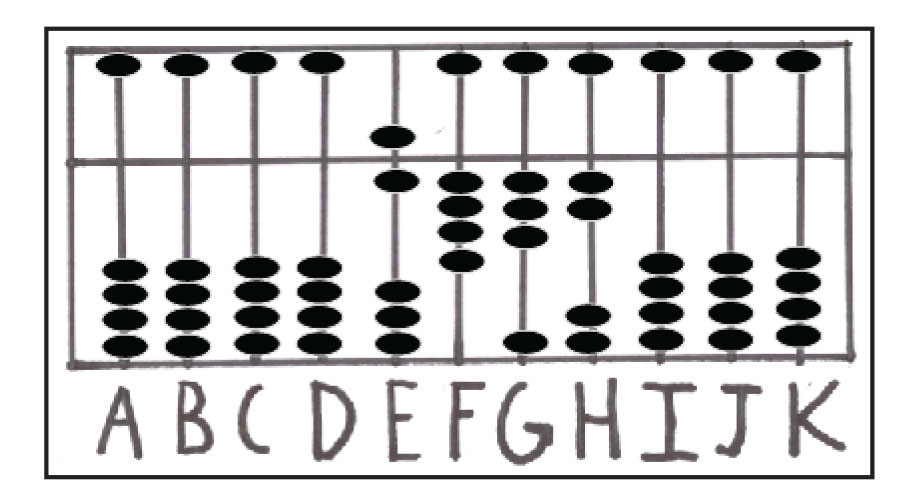شکل شماره ی 15: نمایش عدد 6432 روی میله های EFGH

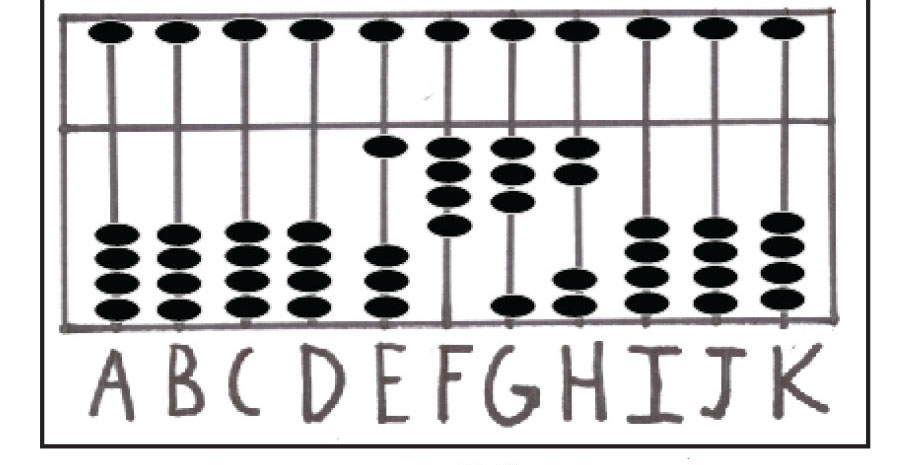شکل شماره ی 16: نمایش عدد 1432 روی میله های EFGH

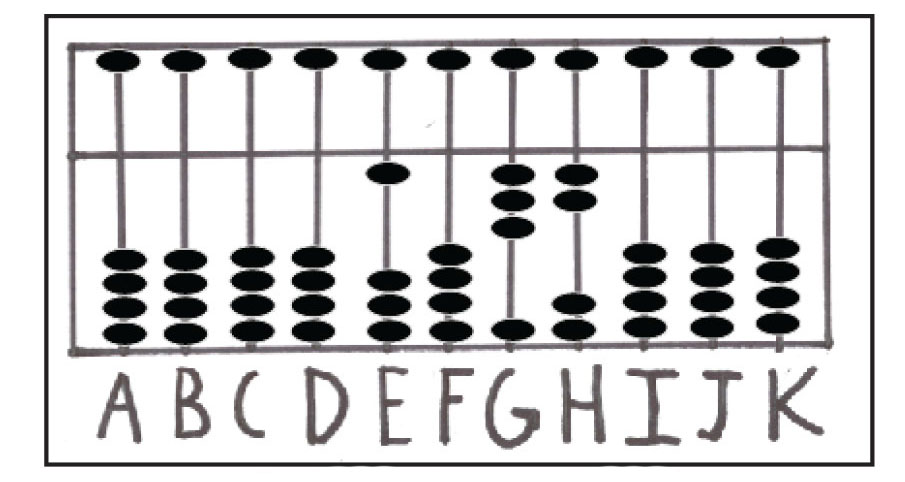شکل شماره ی 17: نمایش عدد 1132 روی میله های EFGH

برای کم­ کردن عدد 6 از میله­ ی دهگان G، متمم 6 یعنی 4 در میله­ ی G اضافه شده و یک مهره از میله­ ی F کم خواهد شد. حالا همانند شکل شماره­ ی 18، عدد 1072 روی چرتکه مشاهده می­ شود. در مرحله ­ی آخر، عدد 1 از میله ­ی یکان H کم می­ شود. پاسخ نهایی 1071 خواهد بود.

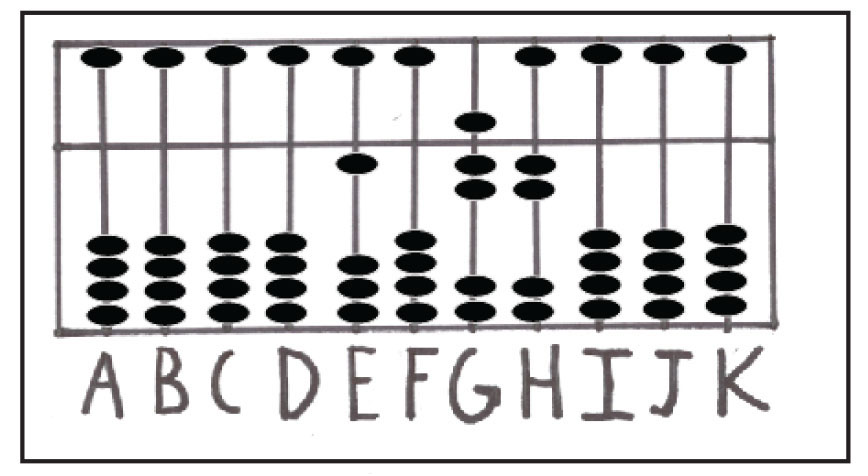شکل شماره ی 18: نمایش عدد 1072 روی میله های FGH

عملیات ضرب

اگرچه مسائل ضرب سخت ­تر از جمع و تفریق هستند، اما با چرتکه­ ی سوروبان به راحتی می­ توان آن­ها را محاسبه کرد. پیش از آنکه دانش­ آموزان بتوانند مسائل ضرب را با موفقیت حل کنند، در ابتدا باید جدول ضرب 9 × 9 را یاد بگیرند. نمایش مضروب و مضروب فیه روی چرتکه، مهم­ترین مرحله­ است. به این ترتیب، نمایش اولین ارقام از میله­ ی یکان آغاز می­شود.

 به عنوان مثال، مسئله ی 4 × 36 را در نظر بگیرید که 36 مضروب و 4 مضروب فیه است. ابتدا انگشت خود را روی میله­ ی یکان H قرار می­دهیم و به سمت چپ چرتکه، نخست ارقام مضروب فیه (موقعیت 1 نسبت به میله ­ی G) و سپس ارقام مضروب (موقعیت 2 نسبت به میله­ ی E) را می­زنیم (هفلفینگر و فلوم، 2011). سپس، عدد 4 را روی میله­ ی B نمایش می­دهیم. در این صورت، فضای کافی در اختیار دانش­ آموزان قرار می­گیرد تا مضروب و مضروب فیه را از هم تشخیص دهند (شکل شماره 19).

انجام مسائل ضرب فقط با جمع ­کردن حاصل ضرب ارقام صورت می­گیرد. در مرحله ی اول، عدد 6 در 4 ضرب می­شود و این حاصل ضرب در میله­ های سمت راست مضروب یعنی روی دو میله­ ی GH جمع می­شود. برای نشان دادن عدد 6، میله­ ی F را صفر می­ کنیم. این مراحل در شکل شماره­ ی 20 نشان داده شده ­اند.

همین فرآیند برای ضرب 30 در 4 نیز اجرا می­ شود. حاصل ضرب این اعداد یعنی 120 در میله­ های EFG اضافه می­شوند. برای نشان دادن عدد 30، میله ­ی D را صفر می­کنیم. به این ترتیب، باتوجه به شکل شماره ­ی 21، حاصل ضرب نهایی یعنی 144 روی میله­ های FGH به دست می ­آید.

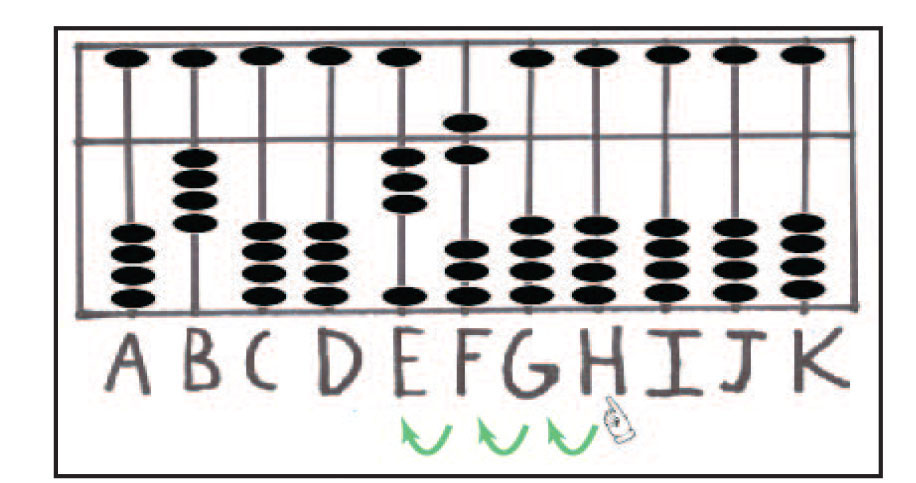شکل شماره ی 19: نمایش مسئله ی 4 × 36

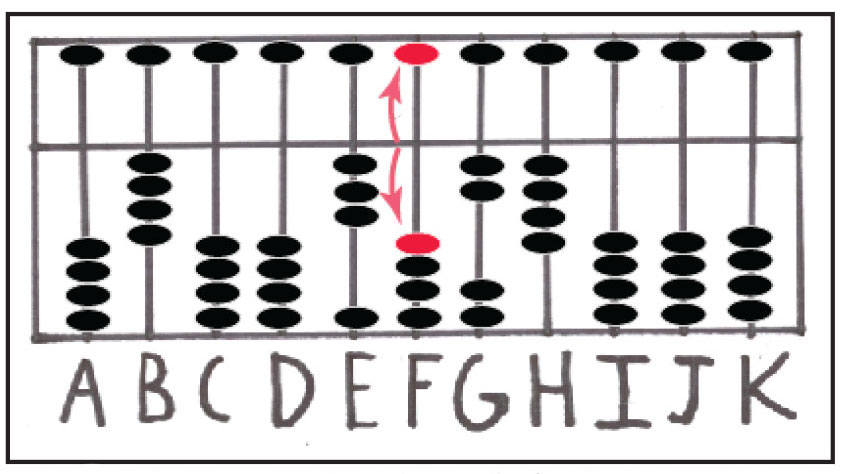شکل شماره ی 20: حاصل 24 روی میله های GH با صفر کردن میله ی F

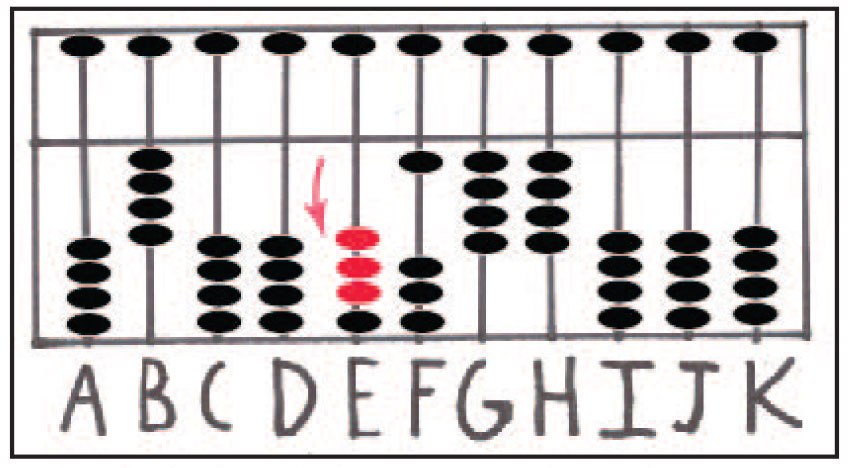
شکل شماره ی 21: حاصل 144 روی میله های FGH با صفر کردن میله ی D

عملیات تقسیم

حل مسائل تقسیم با چرتکه ­ی سوروبان همانند انجام این محاسبات با کاغذ و مداد است. بعلاوه، در این فرآیند از عملیات جمع، تفریق و ضرب استفاده می شود که در بخش­ های پیشین درباره ­ی آن­ها بحث شد. به طور مثال، مراحل حل مسئله­ ی 5 ÷ 19 را به صورت تصویری نشان می­دهیم که کار ما را با فرآیند سنتی محاسبه با کاغذ و مداد مرتبط می­سازد که بسیاری از مدرسان با آن آشنایی دارند.

همان­طور که در اشکال 22-25 مشاهده می ­شود، حل مسائل تقسیم با چرتکه، جایگزین محاسبه با کاغذ و مداد شده است که تجرب ه­ای فیزیکی و ملموس ­تر برای کودکان به حساب می ­آید.

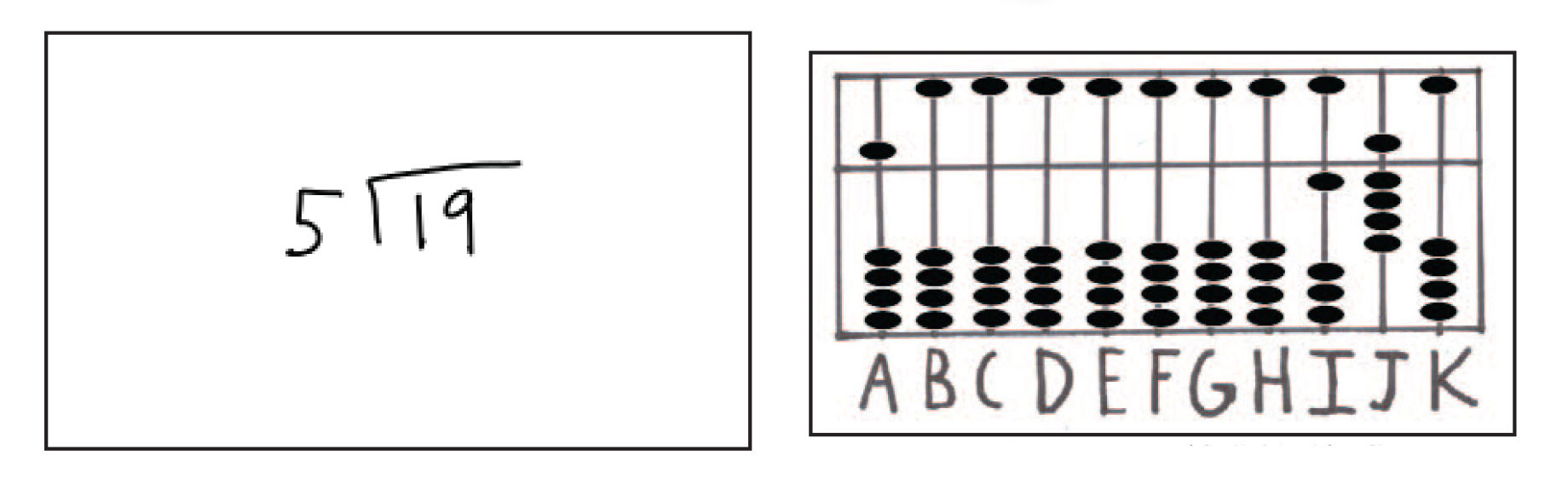شکل شماره ی 22: نمایش مسئله ی 19 تقسیم بر 5

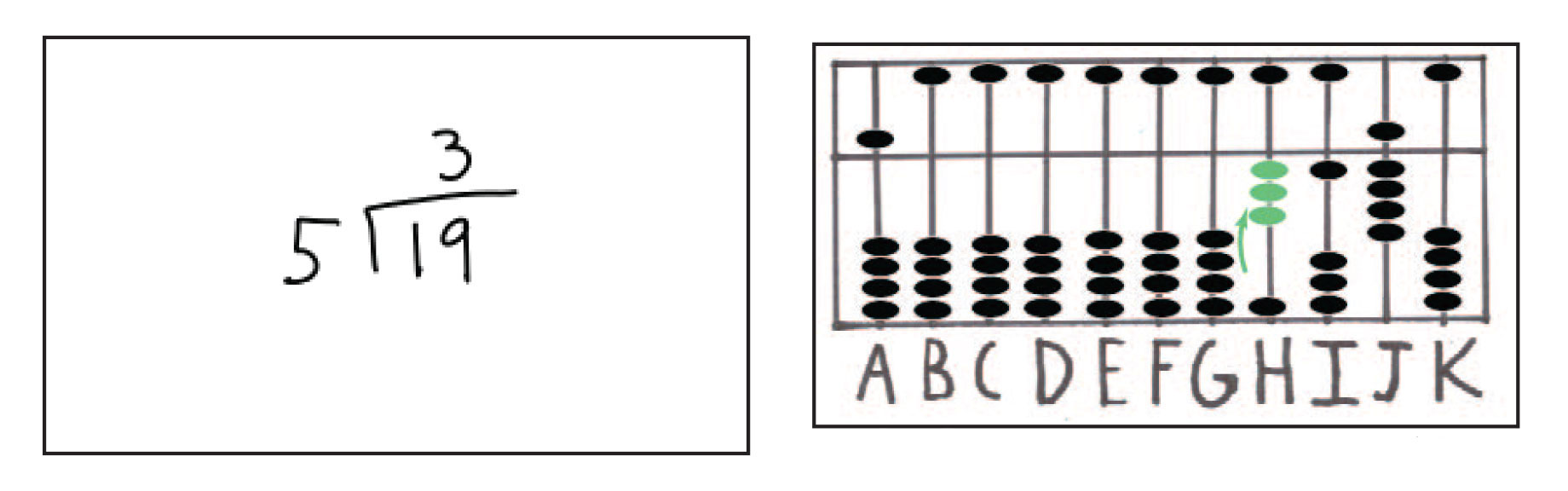شکل شماره ی 23: محاسبه ی مسئله ی 19 تقسیم بر 5 که جواب آن 3 می شود

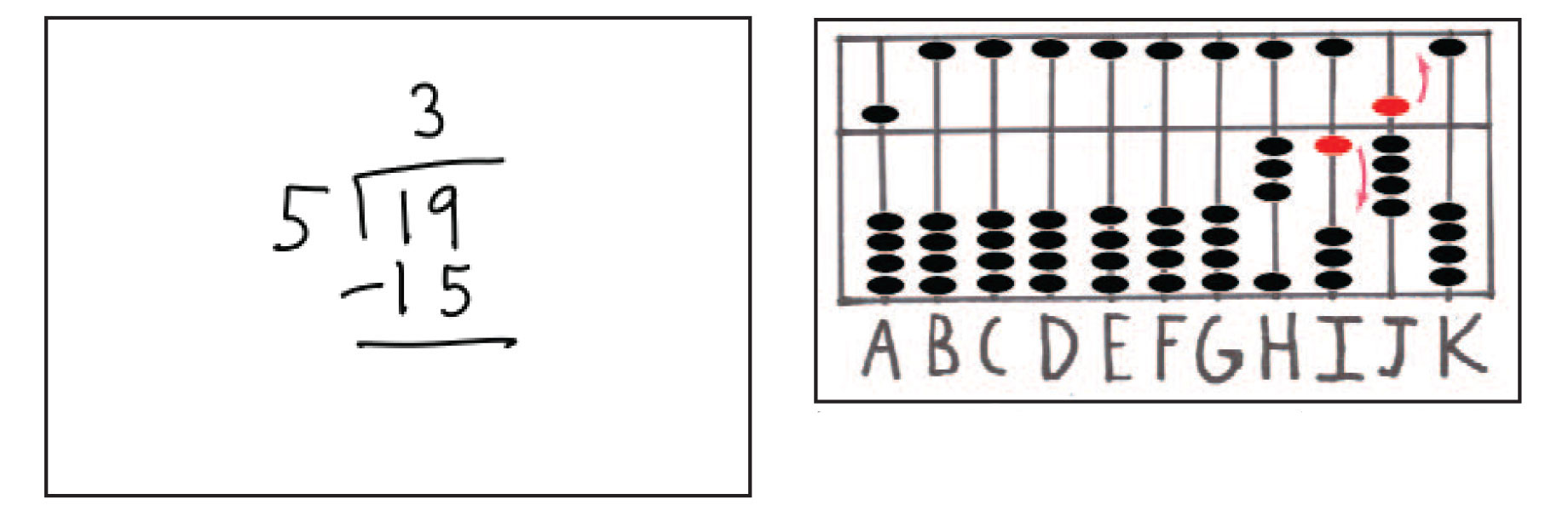شکل شماره ی 24: ضرب مقسوم علیه بر خارج قسمت و تفریق اعداد حاصل از تقسیم

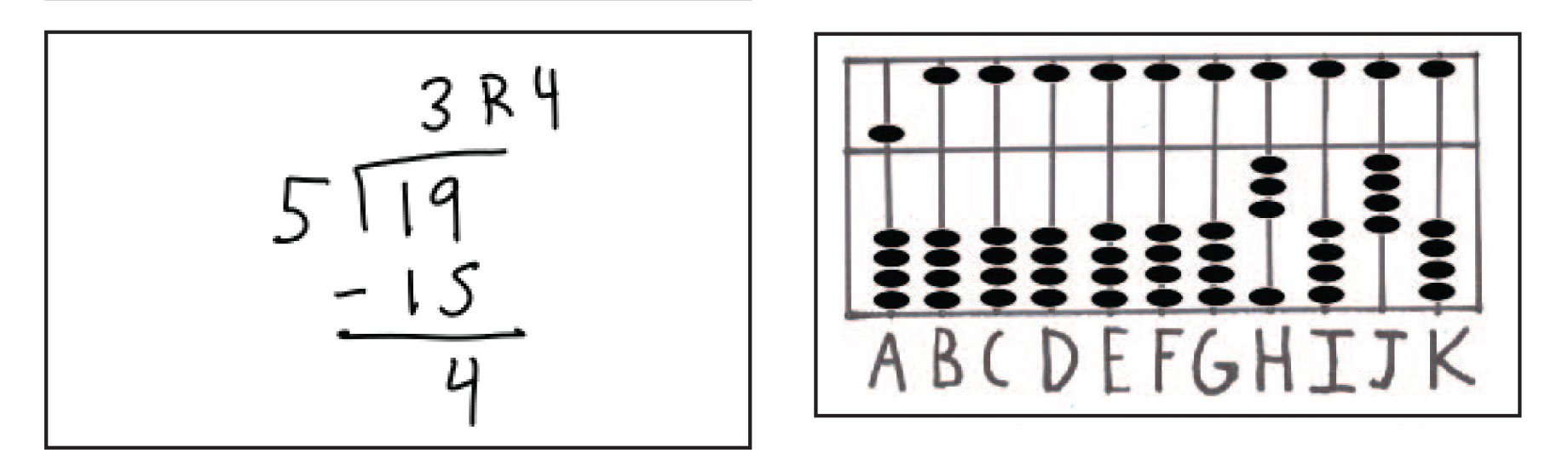شکل شماره ی 25: پاسخ 19 تقسیم بر 5

نتیجه­ گیری

ابزار چرتکه نقش مهمی در انجام محاسبات ایفا کرده است و امروزه نیز همچنان کاربرد دارد. بازرگانان از این ابزار رایج استفاده می­کردند و آن­را به تمام دنیا معرفی نمودند. قابلیت انعطاف­ پذیری چرتکه به گون ه­ای است که در تمام فرهنگ­ ها کاربرد دارد. فرآیند مکانیکی آن موجب می­شود تا بتوان عملیات جمع، تفریق، ضرب و تقسیم را به درستی و بدون استفاده از مداد و کاغذ انجام داد؛ ابزاری که رقیبی برای ماشین حساب­ های امروزی به حساب می­ آید که چهار عملیات اصلی را انجام می­دهند. چرتکه، دریچه ­ای به گذشته است که امکان انجام محاسبات به همان روش­ هزاران سال پیش را برای کاربران فراهم می کند. بعلاوه، امروزه این ابزار در کلاس ­های درس، جایگزین مداد و کاغذ برای دانش ­آموزان شده است که انجام محاسبات را به صورت فیزیکی برای آنان امکان پذیر می ­سازد.

بازدیدها: 284